DISTORSIÓN
Introducción
Mucho podría escribirse sobre
la distorsión en los amplificadores transistorizados; pero como la baja
distorsión obtenible calculando bien los amplificadores de transistores y
aplicando realimentación es comparable con la de los amplificadores de
válvulas, nos limitaremos a un tratamiento general.
Los
términos amplificación y ganancia son utilizados de forma indistinta. Para
señales sinusoidales o para ciertas componentes sinusoidales de una señal
periódica, la ganancia de voltaje es:
AV = VSALIDA
/ VENTRADA = A e jo
En donde
Av es la relación compleja entre dos fasores. En un amplificador
lineal, A y O son independientes de la amplitud y frecuencia de la señal, y la
señal de salida es un duplicado de la entrada. En la figura, la salida no es
proporcional a la entrada y hay una distorsión no lineal o de amplitud. En
otras palabras A no es constante simple. Como resultado de la distorsión de
amplitud , en la salida hay componentes de frecuencia que no estaban presentes
en la entrada. Un análisis de Fourier de la salida revelaría la presencia de
una “segunda armónica”, una componente de dos veces la frecuencia “fundamental”
de la señal de entrada. La distorsión de amplitud generalmente tiene lugar
cuando se aplican señales excesivamente grandes a los elementos no lineales
como los transistores.
En el
otro extremo está también la distorsión por ruido, señales casuales que no
tienen relación alguna con la entrada. Si la señal de entrada es muy pequeña,
la salida se constituirá principalmente de ruido, y por lo tanto no es un
duplicado de la señal de entrada.
En la
figura que aparece a continuación, la curva de respuesta de frecuencia de un
amplificador de audio indica que hay una distorsión de frecuencia; todas las
frecuencias (dentro de una banda definida) no son amplificadas igualmente. En
otras palabras, A es una función de la frecuencia. Una señal que consiste de
una fundamental de 1Khz, una décima armónica a 10Khz y una centésima armónica a
100Khz tendrá una forma de onda diferente después de ser amplificada. Ningún
amplificador esta totalmente libre de la distorsión de frecuencia.
Si q es una función de la frecuencia, las
amplitudes relativas de las componentes de señal pueden permanecer sin cambios,
pero las posiciones de fase relativas están cambiadas. Como se muestra en la
otra figura, dicha distorsión de fase, cambia se forma de la onda de salida. El
ojo es sensible a esta distorsión, pero el oído no lo es; ordinariamente un ser
humano no puede distinguir entre las dos señales. Por otra parte, el oído es
muy sensible a la distorsión de amplitud o frecuencia.
Las
distorsiones de fase y de frecuencia se deben a los elementos de circuito tales
como las reactancias capacitivas e inductivas que dependen de la frecuencia.
Algunos parámetros de transistores son también dependientes de la frecuencia.
En el diseño de amplificadores no sintonizados o de banda ancha se toman
medidas especiales para reducir la variación en la ganancia con la frecuencia.
Clases de Distorsión
Podemos distinguir entre
distorsión lineal y no lineal; en la primera, la tensión de salida depende de
la frecuencia de la señal de entrada, con tal que su amplitud se mantenga
constante, y la ganancia varía en función de la frecuencia aplicada. Esta
variación tenderá generalmente a disminuir en el extremo de la banda de
frecuencias graves y en el de los agudos. Como ya hemos dicho, el
preamplificador no ocasiona ningún problema con respecto a la distorsión
lineal. Sin embargo, en los transistores de potencia existen aún algunas
limitaciones con respecto a la frecuencia.
Con la distorsión no lineal,
la señal de salida ya no es idéntica a la de entrada, lo que origina
armónicos. La distorsión no lineal puede producirse por las siguientes causas:
a) El circuito de base común o
emisor común está atacado por una fuente de tensión.
b) El valor de b no
es constante, sino que disminuye con valores muy bajos y muy altos de la
corriente de emisor. Incluso con bases alimentadas puramente con corriente la
corriente de colector no será completamente idéntica a la de base.
c) La dos mitades de un
amplificador en contrafase (particularmente en clase B) no son idénticas y los
impulsos de corriente son por eso algo desiguales.
d) La elección incorrecta del
punto de funcionamiento puede producir una sobrecarga en el transistor. Si la
corriente de base se hace demasiado alta, se alcanzará la tensión de codo, lo
que evita que la tensión de colector caiga mas. La tensión de salida se corta
entonces bruscamente. Si la corriente de reposo de base es muy pequeña, la
corriente de base puede hacerse cero durante el ciclo positivo, como resultado
de lo cual el transistor se bloqueará; entonces la tensión de colector es
virtualmente igual a la de alimentación. La tensión de salida se recorta de
nuevo, pero el proceso tiene lugar mucho más gradualmente en esta región,
debido al efecto de la pequeña corriente de base. Los “ bordes agudos ” quedan
más o menos “redondeados”.
e) La aparición del efecto de
intermodulación en los amplificadores de clase B y el efecto de almacenaje de
huecos se producen cuando los transistores trabajan más allá de la frecuencia
limite.
f) La no linealidad de otros
componentes, tales como núcleos de hierro en los transformadores, etc.
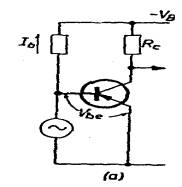
a) La distorsión producida al
excitar un transistor con una fuente de tensión, como en la figura 105,a se
explicará a continuación. Si se conecta entre base y emisor una fuente de
tensi6n de pequeña resistencia interna, la corriente que fluye por el circuito
base‑emisor (y, por tanto, la corriente de colector), quedarán seriamente
distorsionadas, en virtud de la no linealidad de la característica de diodo de
la uni6n base‑emisor.
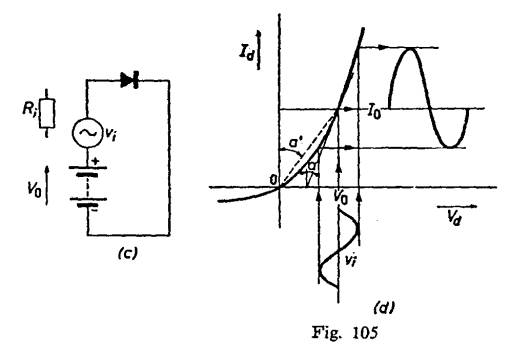
Como puede verse en la
característica ‑Vb ‑Ib de la figura 105,b, la tensión produce una
fuerte distorsión en la corriente de base. En la característica dinámica Ic ‑Ib
vemos que esta corriente produce también una distorsión en la corriente ‑Ic.
Se puede determinar la tensi6n de salida de la característica It ‑Vc,
que como se verá viene muy distorsionada.
Las conclusiones importantes
que se deducen de las características de la figura 105,b son que el grado de
distorsión depende de la mayor o menor excitación y de la corriente de reposo
de base o de emisor. Cuanto mayor sea esta corriente, más dentro de la parte
lineal de la curva se verificará el funcionamiento. La relación entre la
corriente de señal y la de reposo de base nos da la medida de la distorsi6n.
La curvatura de la
característica -Ib ‑Vbe es opuesta a la de la característica ‑Ib ‑Ic
y una puede compensar a la otra en mayor o menor cantidad. La compensación se
efectúa “enderezando” la curva -Ib - Vbe es opuesta a la característica, por el
procedimiento de conectar una resistencia en serie en el circuito de base o
empleando una resistencia de emisor sin estabilizar, de tal manera que se
adapte la curvatura de -Ib -Vbe con la de -Ib -Ic. Esta última tiene un papel
importante en los transistores de potencia; en cambio en los
preamplificadores, como la excitación es tan pequeña, la curvatura de ‑Ib
‑Ic puede ser despreciada. La distorsión será muy pequeña si la base está
excitada con corriente.
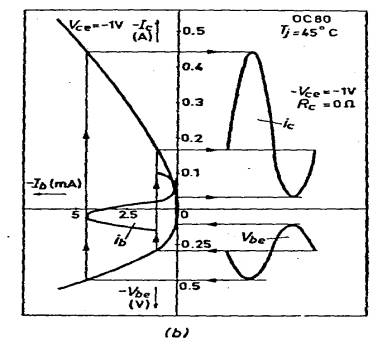
La excitación por la tensión
de la base puede reducirse en su forma más sencilla a un diodo de cristal al
que se aplica una tensión continua para ajustar la corriente y otra alterna para
la excitación. Esto se muestra en la figura 105c.
Con ninguna resistencia más
en el circuito la corriente variará según la característica del diodo de la
figura 105d. Cuando se conoce la característica se puede calcular la distorsión
producida por su curvatura. Daremos a continuación un ejemplo de este cálculo.
La característica del diodo
viene representada por la expresión
qV
Id
= Is ( e kT -1) (94)
donde: Id = corriente del diodo;
Is = corriente de saturación a la temperatura T (la
corriente fluye en sentido inverso, ver figura
12);
q = carga del electrón;
V = tensión aplicada;
R = constante de Boltzmann (1,38 x 10 -23 )
T = Temperatura absoluta (T = 273 + t).
Esta expresión se aplica en
ambas direcciones, tanto en sentido directo como inverso, según sea V positiva
o negativa. Como se verá, cuando T sube, Id disminuye (corriente en sentido
directo). l5 crece mucho más con la temperatura (tiene el mismo papel que Ico
en los transistores). El factor q/kT tiene un valor dado y para t = 25 °C vale
39 V -1.
Esta expresi6n muestra
claramente cuán rápidamente crece la corriente en sentido directo con la
temperatura; incluso con V = 0,2, el exponente será 0,2 x 39 ~ 8 y la corriente
directa, Id = (e8-1) Is = 3.000 Is. Con una corriente de saturaci6n
de 0,5 ILA, la Id será igual a 1,5 mA y subirá para V = 0,4 a un valor no inferior
a 4,5 A. De todos modos, en este punto empezará a tener algún efecto la
resistencia del material semiconductor.
El valor 1 de la fórmula puede
despreciarse frente al término exponencial, quedando:
Id = e 39 .V(e =
2,72)
Is
La aplicación de una tensión
alterna produce una variación DV en V, luego tendremos también una variación DId en
Id:
e39 (V + DV)
= Ib + DId DId = corresponde a la subida de la corriente del diodo
Is
e 39V . e 39DV
= Id ( 1 + DId ) ; h39V es igual a la relación
Id / Is,
Ie
Id
así que:
e39DV
= 1 + DId
. Para valores de DV,
pequeños, se puede desarrollar en serie
1 + 39 DV
+ (39DV)2 + (39DV)3 + … = 1 + DId
1 . 2 1 . 2 . 3 Id
El termino en DV
representa el primer armónico; ( DV)2, el segundo; etcétera.
Nos limitaremos a los dos primeros armónicos:
1 + 39 DV + (39 DV)2
= 1 + DId
1 . 2 Id
La resistencia Rd es igual a DVd/ DId, o
sea, a la experimentada por una pequeña subida de tensión DVd en
el punto de funcionamiento Id, que en la figura 105,d corresponde a tg a. La
resistencia diferencial es distinta de la resistencia en c.c., Vo/Io que es
igual a tg a’,
en la figura 105,d. Estas dos se confunden muy a menudo. Para muy pequeñas
desviaciones de DV,
el término ( DV)2
puede despreciarse V.
Despreciando los segundos términos:
DV = 1 .
DI 39 Id
Si expresamos Id en mA. tenemos: Rd = 25 / Id. (95)
Para un transistor en circuito de
base común, Id será igual a la
corriente de emisor Ie; si se emplea en circuito de emisor común la impedancia
de entrada será alrededor de b veces mayor, es decir Rd ~ 25 / Ib.
Si sustituimos esto en la expresión
anterior, podremos determinar la subida de | + DId I para una tensión | + DV | y
la caida de | - DId
| para una de tensión de | - DV | serán:
+ DId = 1 /Rd [ + DV + 39
(DV)2
]
2
(96)
- DId = 1 /Rd [ - DV +
39 (DV)2
]
2
la amplitud del primer armónico es igual a:
| + DId |
+ | - DId
|
2
y la del segundo será:
Id = | + DId |
+ | -DId
|
4
La distorsión debida al segundo arm6nico es igual al
cociente de la amplitud del segundo armónico por la del primero, o sea:
d2 = DV .
4 . Id . Rd
Cualquier otra resistencia
del circuito deberá sumarse a Rd. Estas suelen ser la resistencia interna de la
fuente, Ri, y la del material de la base, Rbb, que
puede valer 300 Q.
La expresión de la distorsión se
convierte entonces en:
d2 = DV . (97)
4. Id (Rd + Rbb + Ri)
El efecto de la resistencia
extra Ri en la característica del diodo se señala en la figura 105e, donde tg «
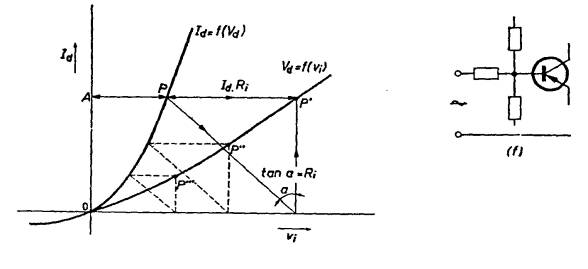
siempre corresponde a la resistencia extra Ri. AP
representa la tensión del diodo
para la corriente OA. La caída de tensión en Ri, o sea Id Ri viene representado
por PP'. Ahora, la nueva característica del
diodo viene representado por OP', que
como puede verse es mucho más recta que la original. Esta nueva característica
puede determinarse sin dificultad
repitiendo este procedimiento para
otros puntos de la línea OP.
Las figuras 105f, g y h dan
diversos métodos para reducir la distorsión. Básicamente es siempre lo mismo:
convertir en excitación por corriente las de
tensión.
En la figura 105f se incluye
una resistencia en el circuito de base para hacer su corriente más lineal; este
mismo resultado se obtiene en la figura 105,g, al no estabilizar la resistencia
de emisor, con lo que se introduce una resistencia aparente de b Re
en el circuito de base.
El sistema de realimentación
introducido en el circuito de la figura 105,h es muy eficaz con excitación de
corriente y tiende a nivelar la distorsión de la
curva -Ib / -Ic, de tal manera que
la tensión de salida sea una reproducción exacta de la corriente de entrada.
Cuando se emplea excitación por tensión, este sistema de realimentación es
ineficaz (ver b).
b). Distorsión debida a la curvatura
de la característica -Ib / -Ic variaci6n de b con excitación por
corriente).
De las características del
transistor en circuito de emisor común puede verse que b no es constante en todo
el margen de funcionamiento, sino que pasa desde grandes excitaciones a
pequeñas. Esto es debido a que muy pequeñas variaciones en el valor de a
pueden producir otras bastante grandes de b. Esto se refleja en la
característica -Ic / -Vc por el espaciamiento entre las líneas de corriente de
base constante, que tiende a ser menor cuanto mayor es la corriente de
colector.
La reducción del valor de a en
el circuito de base común es debida principalmente al menor rendimiento de la
(inyección relación entre la corriente de huecos de emisor a base y la de
electrones en sentido inverso) para altas densidades de corriente. Esto ocurre
debido a una concentración de impurezas relativamente alta en el emisor y una
baja concentración en la base. Si la corriente de huecos crece, la d.d.p. entre
la unión base-emisor lo hará también, como resultado de lo cual los electrones
tienden a ser atraídos hacia el emisor y el rendimiento de la emisión se
reducirá. Esto hace que a baje ligeramente, dando por tanto una considerable
disminución de b.
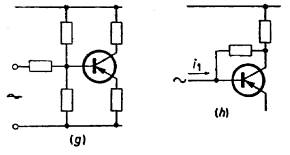
Esto se muestra en la figura
106,a. Deberá notarse que la curva -Ib / -I viene dibujada para una tensión de
colector constante, es decir, para una colector que esté conectado directamente
a la alimentación, mientras que por lo general el colector tiene una carga (ver
también la fig. 29,a). En la figura 106,a, AOB, representa la línea de carga.
La pendiente de las líneas con corriente de base constante se debe a la
realimentación interior de la tensión de colector a la unión base-emisor. Con
altas tensiones de colector, un mayor porcentaje de huecos que cruzan la uni6n
base-emisor alcanzarán el colector y por tanto aumentará la corriente de éste.
Si consideramos solamente la
distorsión debida al segundo armónico (que suele ser admisible), ésta puede
leerse directamente en la característica -Ic / -Vce. El porcentaje de
distorsión será igual a:
d2 = (OB - OA) . 100 %
2.(OB + OA)
Las distancias OA y OB pueden
medirse en el gráfico.
Para
el transistor OC 30, con una carga de colector de 12 Q, una alimentación de 6
V y una corriente de reposo de base de 15 mA (la corriente de colector es
aproximadamente 0,5 A), la distancia OA, con una excitación de unos 1n mA. será
de 13,5 mm y la distancia OB es de 18,5 mm. La distorsión será:
d2
= 18,5 -13,5 = 7,85
por 100
4
(18,5 + 13,5)
que es comparable con la de
los amplificadores de válvulas. En los amplificadores en contrafase, el
segundo (e incluso el cuarto, sexto, etc.) armónico se elimina. Por supuesto,
esto sólo se aplica a los amplificadores de clase A (y en menos extensión a los
de clase AB).
c) Si las dos
mitades de un amplificador de clase B son desiguales en el funcionamiento, los armónicos
pares resultarán muy distorsionados. Si la mitad positiva de la modulación es
igual a 1, (ver fig. 106,c) y la mitad negativa es igual a I" la amplitud
del fundamental o primer armónico será igual a (Il + I2)
/2 y la del segundo, (I1- I2)/4; además, habrá una componente continua que será
igual a la amplitud del segundo armónico. Por tanto, el porcentaje de
distorsión será:
d2 = I1 - I2
.
2.(I1 + I3)
d) La distorsión producida
por intermodulación y almacenamiento de huecos ya ha sido tratada con detalle
(ver fig. 84). En el diseño de un circuito debemos asegurarnos que las subidas
o bajadas de la temperatura variaciones y las de la tensión de batería, etc. no
hagan que las condiciones de funcionamiento de los transistores de potencia se
modifiquen hasta tal punto que ocasionen grandes distorsiones. Particularmente
en los amplificadores clase B, en los que la corriente de reposo es muy
pequeña, una ligera desviación de las condiciones de funcionamiento en reposo
dará marcadas variaciones de la corriente de colector y, por tanto, una gran
distorsión de intermodulación.
Debería
tenerse en cuenta en relación con esto que una corriente de reposo grande no
produce necesariamente un mínimo de distorsión intermodulación, lo que puede
verse en el gráfico de la figura 84,d. Para reducir esta distorsión a un
mínimo, la suma de las pendientes DIb y DVbe, (I + II) en la zona de transición (cuando ambos
transistores trabajan simultáneamente) deberá ser igual a la pendiente de la
curva I o II y esto sólo es posible en un margen muy estrecho. Con una
corriente de reposo demasiado baja se obtiene una distorsión por compresión,
como se muestra en la figura 84,b; y si es demasiado grande, la pendiente en la
zona de transición será doble de la pendiente normal dando una distorsión por expansión. Como este ajuste
es muy crítico, se prefiere que los amplificadores funcionen en clase A con
señales pequeñas; esto se conoce con el nombre de funcionamiento en p A‑B.
Las condiciones de funcionamiento normal pueden hacerse más o menos
independientes de la tensión de batería, incluyendo una lámpara incandescente
entre la alimentación y el punto en que se aplica la polarización negativa (en
serie con Rl, en la fig. 81,a). Cuando la tensión de la batería
aumenta, también lo hará la resistencia de la lámpara; como consecuencia, la
corriente que pasa por la lámpara y la polarización negativa permanecerán más
o menos constantes.
Además,
la lámpara funciona como estabilizador de temperatura. Cuando la temperatura
ambiente sube, la resistencia del filamento crece también, como resultado de lo
cual la corriente baja, reduciendo el efecto de la subida en Ico. En vista de
que la lámpara funciona con una temperatura bastante alta, el efecto de
compensación de la temperatura ambiente será sólo muy pequeño.
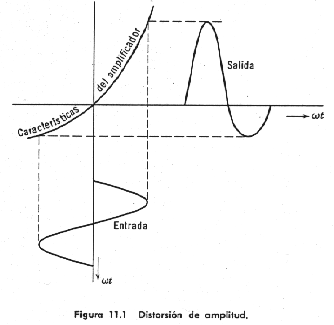
En
la fig. 11.1, la salida no es proporcional a la entrada y hay una distorsión no
lineal o de amplitud. En otras palabras, A no es constante simple. Como
resultado de la distorsión de amplitud, en la salida hay componentes de
frecuencia que no estaban presentes en la entrada. Un análisis de Fourier de la
salida revelaría la presencia de una "segunda armónica", una
componente de dos veces la frecuencia "fundamental" de la señal de
entrada. La distorsión de amplitud generalmente tiene lugar cuando se aplican
señales excesivamente grandes a los elementos no lineales como las válvulas y
los transistores.
En el otro extremo está la
distorsión debida al ruido, señales casuales que no tienen relación alguna con
la entrada. Si la señal de entrada es muy pequeña, la salida consistirá
principalmente de ruido y no es un duplicado de la entrada.
La "nieve" que
aparece en la pantalla de televisión cuando sólo está disponible una señal muy
débil, es una representación visual del ruido. Una de las fuentes del ruido es
el movimiento térmico casual de los electrones en los elementos del circuito
del amplificador. El efecto de disparo de los electrones individuales que
llegan a la placa en una válvula al vacío es otra fuente de ruido. El ruido
adquiere gran importancia en los pasos de entrada en donde los niveles de señal
son pequeños; cualquier ruido que entre ahí es amplificado por todos los pasos
subsecuentes. El rango dinámico de cualquier amplificador está limitado en un
extremo por el nivel al que las señales son obstruidas por el ruido y en el
otro extremo por el nivel al que la distorsión de amplitud llega a ser
excesiva.
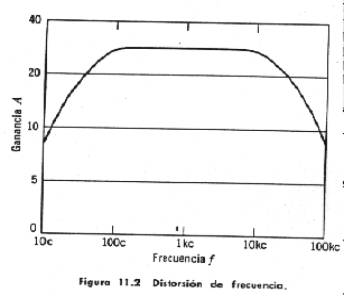
En
la fig. 11.2, la curva de respuesta de frecuencia de un amplificador de audio
indica que hay una distorsión de frecuencia; todas las frecuencias (dentro de
una banda definida) no son amplificadas igualmente. En otras palabras, A es una
función de la frecuencia. Una señal que consiste de una fundamental de 1 kc,
una décima armónica a 10 kc y una centésima armónica a 100 kc tendrá una forma
de onda diferente después de ser amplificada. Ningún amplificador está
totalmente libre de la distorsión de frecuencia
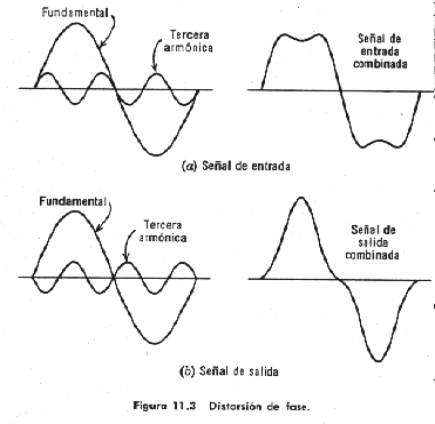
Si
q
es una función de la frecuencia. Las amplitudes relativas de las componentes
de señal pueden permanecer sin cambios, pero las posiciones de fase relativas
están cambiadas. Como se muestra en la fig. 11.3, dicha distorsión de fase,
cambia la forma de la onda de salida. El ojo es sensible a esta distorsión,
pero el oído no lo es; ordinariamente un ser humano no puede distinguir entre
las dos señales. Por otra parte, el oído es muy sensible a la distorsión de
amplitud o frecuencia.
Las
distorsiones de fase y de frecuencia se deben a los elementos de circuito tales
como las reactancias capacitivas e inductivas que dependen de la frecuencia.
Algunos parámetros de válvulas y transistores son también
dependientes de la frecuencia.
En el diseño de amplificadores no sintonizados o de banda ancha se toman
medidas especiales para reducir la variación en la ganancia con la frecuencia.
Cálculo de los coeficientes
de Fourier
Pueden utilizarse métodos diferentes
para calcular los coeficientes B0, B1, B2,
etc. Vamos a describir el método debido a Espley, que es sencillamente una
generalización del procedimiento de la sección anterior. En esta sección
supusimos que solamente tres términos, B0, B1, y B2,
de la serie de Fourier eran distintos de cero. Estas tres componentes se
calcularon en función de las tres corrientes, Imax, Imin e Iy. Como una
aproximación mejor, supongamos que existen solamente cinco términos, B0,
B1, B2, B3 y B4, en la serie de
Fourier resultante. Para calcular estos cinco coeficientes, se necesitan los
valores de la corriente para cinco valores diferentes de x. Estos se eligen
para intervalos iguales de la señal de entrada. Entonces
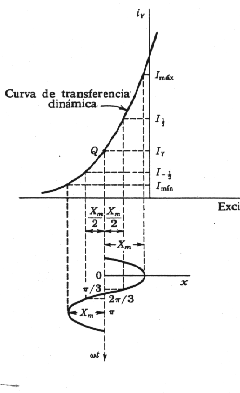
Imax, I 1/2, Iy, I
-1/2, Imín corresponden, respectivamente, a los valores siguientes
de x: el valor máximo positivo, la mitad del valor máximo positivo, cero, la
mitad del valor máximo negativo y el valor máximo negativo. Estos valores se
representan en la figura 18‑3.
Suponiendo una señal de
entrada de la forma x=Xm, cos wt, como la representada,
cuando wt = 0 : iy = Imax
cuando wt = p/3 : iy = I 1/2
cuando wt = p/2 : iy = Iy
cuando wt = 2.p/3 : iy = I -1/2
cuando wt = p : iy = Imin
Introduciendo estas
condiciones en la ecuación (18‑16), resultan cinco ecuaciones con cinco
incógnitas. Resolviendo estas ecuaciones, se obtiene que :
B0 = 1/6 (Imax + 2.I 1/2
+ 2.I -1/2 + Imin) -
Iy
B1 = 1/3 (Imax + I 1/2
- I -1/2 - Imin)
(18
- 18)
B2 = 1/4 (Imax - 2.Iy +
Imin)
B3 = 1/6 (Imax - I 1/2
+ 2.I -1/2 - Imin)
B4 = 1/12 (Imax - 4.I 1/2
+ 6ly - I ‑1/2 + Imin)
La distorsión de cada armónico se
define como :
D2 = |B2|
|B1|
D3 = |B3|
(18 -19)
|B1|
D4 = |B4|
|B1|
donde Ds (s = 2,3,4, ...)
representa la distorsión del armónico s.
Potencia de salida. Si la
distorsión no es despreciable, la potencia entregada a la frecuencia del
fundamental es :
P1 = B12 . Rl (18 - 20)
2
Sin embargo, la potencia de salida
total es :
P = (B12 + B22 + B32
…) Rl = (1 + D22 + D32 + …).
P1
2
(18 - 21)
P = (l + D2). P1
donde
la distorsión total, o factor de distorsión, se define como :
D = Ö D22 + D32 + D42 +
… (18‑22)
Si la
distorsión total es del 10 %,
P = [ 1 + (0, 1)2] P1 = l,0l P1
La
potencia de salida total es solo un 1 % superior a la del fundamental cuando la
distorsión es del 10 %. Por tanto, se comete poco error utilizando solamente
el término fundamental Pl para calcular la potencia de salida. Sin
embargo, puede cometerse un gran error si se utiliza la ecuación (18‑S)
en lugar de la (18‑20) para calcular la potencia. La primera se basa en
la suposición de que la componente fundamental B, puede calcularse mediante la
ecuación (18‑12) en lugar de la fórmula (18‑18), más exacta.
De
paso, digamos que la distorsión armónica total no es necesariamente un índice
de la poca calidad de una audición musical. Habitualmente, la misma cantidad de
distorsión es más desagradable cuanto mayor es el orden del armónico.‑
Medición de la distorsión alineal por
intermodulación. (Método SMPTE).
Un
segundo método para medir la distorsión alineal consiste en aplicar
simultáneamente dos ondas senoidales de diferentes frecuencias a la entrada del
amplificador y observar las frecuencias suma, diferencia, y de combinación,
producidas por la alinealidad del amplificador. Esta manera de encarar el
problema de la evaluación de la distorsión se llama método de intermodulación.
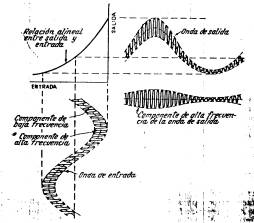
Si bien las frecuencias de
señal pueden combinarse de muchas maneras, hay dos casos que merecen atención
particular. En el primero, una señal de prueba de baja frecuencia y otra de
alta frecuencia de amplitud algo menor, se aplican simultáneamente al
amplificador. De haber efectos alinéales, la amplificación experimentada por la
componente de alta frecuencia f2 varía l al ritmo de la frecuencia
f1 de la señal de baja frecuencia, según lo ilustra la Fig. 8‑20.
Por lo tanto, la onda de frecuencia J~ en la salida del amplificador estará
modulada por la baja frecuencia f1. El importe de la distorsión se expresa
entonces en términos de esta modulación de la onda de alta frecuencia, de
acuerdo con la relación
Distorsión de intermodulación
(método SMPTE),tanto por ciento :
100 . Ö m12
+ m22 + … (8 -
7a)
donde m1 es el grado (le modulación que la
componente de salida de frecuencia f2 sufre a la frecuencia f1, y m2
la correspondiente modulación de f2 a la frecuencia 2f1.
Este método particular de
emplear dos señales para determinar la distorsión alineal se usa ampliamente en
los sistemas de audiofrecuencias asociados con las instalaciones de cine
sonoro. Se lo conoce generalmente con el nombre de método SMPTE, por haber sido
normalizado por la Society of Motion Picture and Televisión Engineers.2
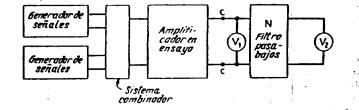
La
Fig. 8‑21 ilustra un equipo para medir la intermodulación por el método
SMPTE. El sistema para combinar las salidas de dos generadores de señales puede
adoptar una de muchas formas posible, tal como la de un transformador con
primario provisto de punto medio, o dos válvulas amplificadoras con entradas
independientes e impedancia común de carga. Como alternativa, puede usarse un
generador de señales de dos frecuencias especialmente preparado para estos
ensayos 3. La red N1 separa la alta
frecuencia y sus bandas laterales de
las otras componentes que pueden hallarse presentes en la salida del
amplificador. El voltímetro Vl mide la amplitud media de esta onda modulada resultante, es decir, mide la
amplitud E2 de la portadora en la Fig. 8‑19b. La componente de modulación
de la envuelta se determina entonces rectificando la onda modulada, separando
la componente de frecuencia de modulación de la envuelta mediante el filtro
pasa bajos N2 y determinando la amplitud de la componente de modulación por
medio del voltímetro V2. Se advertirá que los aparatos encerrados en el
rectángulo de línea cortada en la Fig. 8‑21 representa un sistema para
medir las características de una onda
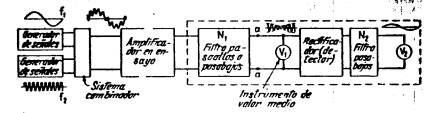
modulada. La calibración
puede realizarse aplicando tensiones conocidas de frecuencias fl y f2 a los
terminales aa.
Con
un sistema de medición tal como el ilustrado en la Fig. 8‑21, la práctica
usual consiste en hacer la señal de prueba de baja frecuencia cuatro veces
mayor que la señal de prueba de alta frecuencia aplicada al sistema. La baja
frecuencia está por lo general comprendida entre 6~) y 100 ciclos, mientras que
la alta frecuencia es por lo común de 5.000 ciclos o más. La red N2 debe tener
un ancho de banda suficiente como para dejar pasar las bandas laterales de
segundo orden, es decir, la frecuencia 2fl; la red Nl debe tener un ancho de
banda correspondiente, es decir, un valor mayor que 4f1. El voltímetro Vl debe
ser del tipo de valor medio; resultan satisfactorios los voltímetros con
rectificadores de óxido de cobre. Por su parte, el voltímetro V~ es idealmente
un voltímetro de ley cuadrática, pero se obtienen resultados satisfactorios
para las necesidades ordinarias empleando un instrumento de valor medio a
rectificador de óxido de cobre. Sin embargo, nunca debe utilizarse un
voltímetro de cresta en V,.
El
valor numérico de la distorsión por intermodulación determinado por el método
SMPTE depende principalmente de la alinealidad encontrada por la señal de
prueba de baja frecuencia, debido a que esta señal es la mayor en las
condiciones normales de ensayo. La distorsión por intermodulación observada es
en gran parte independiente del valor de la frecuencia mayor f2, pero depende
por lo menos de cierta medida del valor de f1, particularmente cuando f1 es lo
suficientemente baja como para caer en la región en que la respuesta del
amplificador comienza a disminuir.
Medición de la distorsión
alineal por intermodulación. (Método CCIF)
En
el segundo método de ensayo de intermodulación, las dos señales de prueba
tienen iguales amplitudes y son de frecuencias relativamente altas pero poco
diferentes. Cuando hay distorsión alineal, aparece una componente de
frecuencia diferencia en la salida, la que se utiliza para medir la distorsión
presente. La situación está ilustrada en la Fig. 8‑19c, donde fn y fb
representan las dos frecuencias de pruebas de amplitudes En y Eb, y donde Ed
es la amplitud de la componente de frecuencia diferencia resultante fd2. La
distorsión por intermodulación se expresa cuantitativamente en este caso
mediante la relación
Distorsión de
intermodulación = Ed
. x 100 (8 - 8)
(método CCIF), tanto por
ciento Ea + Eb
esta forma del ensayo de
intermodulación ha sido recomendada por el Comité Consultivo Telefónico
Internacional.
La Fig. 8‑22 ilustra la
instalación necesaria para el ensayo de intermodulación según el método CCIF.
La componente de frecuencia diferencia Ed se separa por medio del filtro
pasabajo N, y se mide mediante el voltímetro V2. Las amplitudes de las señales
de prueba E. y Eb que aparecen en la Ec. (8‑7) se miden con ayuda del
voltímetro V.: si V. es un voltímetro de cresta, la tensión de cresta
observada en los terminales cc representa aproximadamente el valor de cresta
de Ea + Eb. Como alternativa, EA Y Eb pueden determinarse individualmente
aplicando independientemente las tensiones de prueba a los terminales del
amplificador y observando los valores correspondientes en Vi.
Al hacer un ensayo de intermodulación según
el método CCIF, las frecuencias de ensayo fn Y fb se eligen por lo general
cerca del extremo de alta frecuencia de la gama de respuesta y a veces se
disponen expresamente en la región donde la respuesta de alta frecuencia
comienza a caer apreciablemente. La diferencia fd = fb ‑ fb entre las dos
frecuencias de ensayo es por lo común moderadamente baja, por ejemplo de 60 a
200 ciclos. Esta frecuencia diferencia no debe ser tan baja como para ser menor
que el límite inferior de frecuencias del amplificador, pues de lo contrario
los circuitos del amplificador tenderían a suprimir la salida en la frecuencia
diferencia.
Los
valores de la distorsión por intermodulación observados según el método de la
CCIF son indicativos de las distorsiones alineales existentes en la región del
espectro correspondiente a las frecuencias fa y fb. En particular, el método
de la CCIF es capaz de medir las consecuencias de la distorsión alineal
presente cerca del límite superior de frecuencias del amplificador, allí donde
la respuesta comienza a caer.
El
valor observado de la distorsión por intermodulación es substancialmente
independiente del valor exacto de la frecuencia diferencia fa - fv = fd siempre
que esta diferencia sea una fracción pequeña de las frecuencias de ensayo y
siempre, además, que la frecuencia diferencia fd no caiga en la zona de la
curva de respuesta en que la ganancia del amplificador comienza a caer
apreciablemente.
Comparación
entre los diferentes métodos de medición alineal. Cuando la distorsión alineal
es pequeña y no dependiente de la frecuencia, los tres métodos de medición
delineados más arriba conducen a resultados concordantes y no hay razón para
preferir ninguno de ellos. Vale decir que los resultados obtenidos con uno de
los métodos pueden transformarse en resultados de otro mediante la aplicación
de factores numéricos adecuados. Así, si un amplificador asimétrico ( es decir,
no push‑pull ) se prueba en estas condiciones y si se asegura que en las
tres condiciones de prueba se desarrolle la misma tensión total de cresta en la
salida, los resultados de las Ecs. (8‑7) y (8‑8) serán iguales,
respectivamente, a 3,2 y 0,5 veces el resultado obtenido mediante la Ec. (8‑6).1
Sin embargo, cuando la
distorsión alineal depende de la frecuencia, los distintos resultados no están
ya directamente relacionados unos con otros y 1ampoco serán idénticas las
correlaciones con las pruebas de audición.
Ello
se debe a que el método armónico observa directamente la medida en que resulta
distorsionada una onda senoidal de frecuencia determinada, mientras que en los
métodos por intermodulación se presta atención a la distorsión que resulta de
la interacción entre distintas frecuencias. En el método SMPTE se atiende
especialmente a los efectos producidos sobre las componentes de alta frecuencia
de la señal por las componentes intensas de baja frecuencia cuando hay
alinealidad en las frecuencias bajas. En contraste, el método de la CCIF pone
de relieve las componentes de distorsión de baja frecuencia que resultan de la
distorsión alineal de las componentes de alta frecuencia de la serial.
Estos
diferentes tipos de distorsión ejercen efectos sicológicos distintos sobre el
oyente. Dado que los tres tipos de distorsión se hallan simultáneamente
presentes cuando se amplifica una onda sonora compleja, es posible que ninguno
de ellos pueda proveer un valor numérico que se correlacione exactamente con
los ensayos auditivos en una variedad de condiciones. En general, cuando el
ensayo debe ser único, el de intermodulación es por lo común más útil que el
armónico. No obstante, para obtener una idea completa del comportamiento
alineal del sistema es necesario hacer los dos ensayos de intermodulación y con
varias combinaciones de frecuencias en cada caso. De hacerse el ensayo de
distorsión armónica, debe repetírselo para diversas frecuencias fundamentales,
incluyendo la correspondiente a la frecuencia baja del ensayo de
intermodulación según SM PTE.
El nivel de distorsión
tolerable en un sistema de audiofrecuencias depende de la naturaleza del sonido
de que se trate y de una variedad de factores sicológicos. Es posible reconocer
auditivamente una distorsión armónica de 1 por ciento, pero para que la
distorsión armónica resulte seria, ella debe ser mayor que alrededor del 10 por
ciento. Se pueden tolerar distorsiones armónicas todavía mayores si ocurren
principalmente en las frecuencias menores que 100 ciclos o mayores que 4000. La
intermodulación, según se la determina por el método SMPTE, no puede
reconocerse a menos que exceda del 10 por ciento cuando el tono de baja
frecuencia está por debajo de los 100 ciclos; en cambio, cuando el tono de baja
frecuencia es de algunos centenares de ciclos, es ya perceptible una
distorsión de 3 ó 4 por ciento. La intermodulación determinada según el método
CCIF puede ya reconocerse auditivamente cuando su nivel es de una fracción de 1
por ciento y es ya muy seria si llega al 3 ó 4 por ciento cuando las frecuencias
de ensayo están comprendidas entre 400 y 5000 ciclos, debido a la mayor
sensibilidad del oído a estas frecuencias.