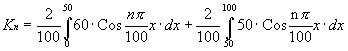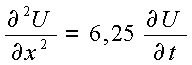Problemas de Contorno

· Ejemplo 1

60 si 0 < x < 50

50 si 50 < x < 100

· Una de las maneras de resolver este tipo de problemas consiste en plantear la funcion dependiente de dos variables como el productu de dos funciones dependientes cada una de una variable (Variables Separables).

Es decir:

· Entonces la Ecuacion del problema queda:

Y separando Variables Obtenemos:

(Notamos que si Es Cte. Significa que las variables pueden ser separadas ya que

cada uno de los cocientes puede variar en forma independiente)

· Si el metodo es correcto solo queda evaluar los posibles casos del coeficiente. Para ello separamos en dos ecuaciones diferenciales.

1 2

· Se entiende que es la condicion =0 habiendo aplicado separacion de variables con lo cual queda por lo tanto si para cualquier t da 0 entonces

· Evaluamos los casos Posibles del parametro resolviendo la ecuacion diferencial 1 en cada uno de los casos

Si < 0

Dado que la unica solucion es la trivial

Si = 0

Es posible el valor 0

Si > 0

· De la Ecuacion 2 tenemos:

La solucion de esta ecuacion diferencial de 1º Orden sera:

· Recordando que: Escribimos El Producto de las respectivas ecuaciones donde de fusionan las constrandes En un unico K_n

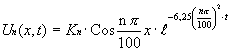
· Notese que U_n(x,t) solo representa uno de los infinitos valores de la funcion para un solo valor de n, por lo cual la solucion correcta sera

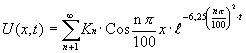
· Ahora solo queda determinar el termino K_n para lo cual utilizaremos la condicion de contorno que nos queda.

En esta condicion nos dicen que y reenplazando en la U(x,t) hallada se obtiene:

Si Observamos esta ultima expresion veremos que K_n es el coeficiente del desarrollo en serie de fourier en senos de la funcion f(x). Y lo hallamos como tal.